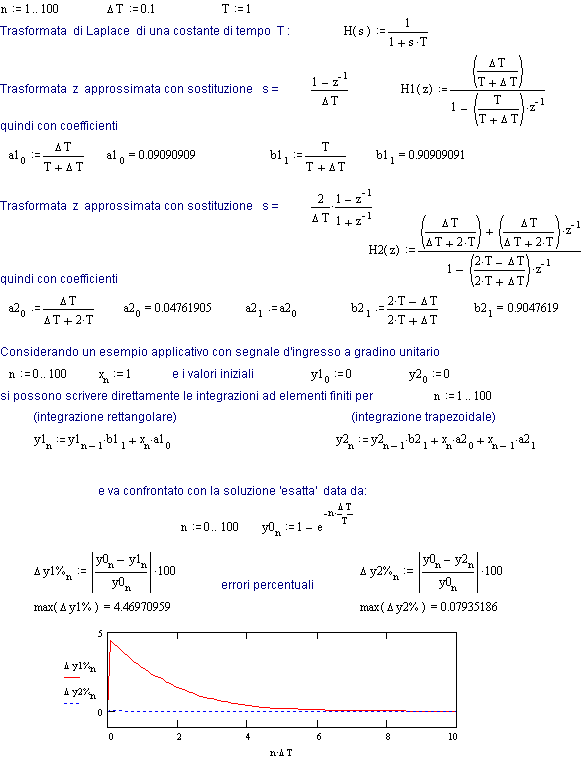Capitolo 17 ) Conversione delle strutture da continue a discrete
Per trasformare una tradizionale struttura di tipo analogico in una equivalente struttura di tipo digitale esistono fondamentalmente due diversi approcci: il primo è l’ invarianza all’impulso ed il secondo la trasformazione bilineare.
Con il primo si impone che la risposta all’impulso del sistema digitale debba uguagliare quella del corrispondente sistema analogico.
Se il segnale d’ingresso è l’impulso d, l’uscita rappresenta la trasformata della funzione stessa, cioè h (vedi fine del capitolo 4).
Nel semplice
caso di una costante di tempo T si ha che
h t = e -t/T , ma
considerando il tempo discreto t
= n·DT diventa
h n = e -n·DT/T.
La
trasformata z di questa è
H(z)
= S
hn·z-n = S (e
-DT/T· z -1)
n
Sviluppando la serie geometrica[1]) si ha
![]()
quindi i coefficienti della struttura generalizzata sono a0 = 1 e b1 = e-DT/T
Anche se si può dimostrare che qualsiasi funzione può essere trasformata in somme di termini di questo tipo, tale soluzione è piuttosto laboriosa.
Una possibile approssimazione che facilita la soluzione è data dall’uguaglianza del ritardo unitario in termini di trasformata s di Laplace rispetto alla trasformata z . Un puro ritardo di tempo DT ha la trasformata s uguale a e -DT·s (vedi tabella al capitolo 7, con n=1), mentre l’analoga trasformata z è semplicemente uguale a z -1, quindi si può scrivere
z -1 = e -DT·s
Sviluppando il secondo membro in serie ed approssimando questa serie ai primi due termini[2])[S1], si ha
z -1 @ 1 - DT·s
da cui si può ricavare
![]()
Con tale approssimazione è possibile ricavare la trasformazione z
di una funzione in s qualsiasi semplicemente
sostituendo ogni s di questa con l’analoga
espressione in z.
Ad esempio nel caso precedente la funzione
![]()
potrebbe essere trasformata
in
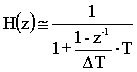
da cui si possono ricavare i coefficienti della struttura generalizzata
![]() e
e ![]()
coincidenti con quanto ottenuto direttamente con l’applicazione delle differenze finite (vedi pag. 16-1).
Si ritiene opportuno ribadire che questo metodo è semplice, ma solo approssimato e può essere visto come metodo d’integrazione rettangolare.
Considerando infatti il caso del segnale d’uscita y come integrale del segnale d’ingresso x , cioè
![]()
l’integrazione può essere svolta numericamente come yt = yt-1+ DT·xt .
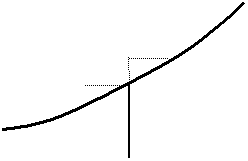
La Fig. 17.1 illustra graficamente il significato di questa operazione: il segnale x campionato ogni DT rappresenta una serie di rettangoli di larghezza DT e di altezza xn·DT , dove n è il numero del campionamento.
Al generico istante t = n·DT si avrà un’uscita yt che sarà la somma del valore raggiunto all’istante precedente yt-1 e dell’area del rettangolo DT·xt .
Ovviamente nella figura l’intervallo DT è esagerato: la precisione del metodo dipende da quanto questo è piccolo, in modo da approssimare il più possibile con piccoli scalini l’andamento di x.
![]()
![]()
![]()
DT
![]()
t-1 t
Fig.17.1 - Principio d’integrazione approssimata rettangolare
Se ora si esprime la stessa operazione in termini di trasformate z si ha:
y(z) = y(z) · z-1
+ DT · x(z) cioè ![]()
Se invece si fosse espressa in termini di trasformate s di Laplace, l’operazione di integrazione (in questo caso continua), si sarebbe ottenuto:
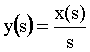 cioè
cioè 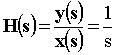
Come si vede uguagliando i due tipi di trasformate, si è riottenuta l’equivalenza in z dell’operatore s.
Ma questo permette anche una diversa soluzione. Se l’integrazione anzichè rettangolare fosse stata un’integrazione trapezoidale l’equivalenza sarebbe di altro tipo (e più approssimata).
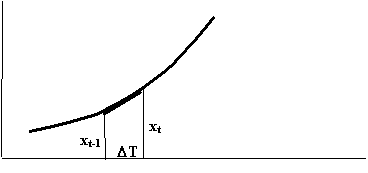
La Fig. 17.2 illustra tale alternativa, in cui al tempo t viene sommata ad yt-1 l’area del trapezio formato con i due valori xt-1 e xt. L’approssimazione è dunque la linearizzazione dell’andamento di x durante l’intervallo DT, che risulta ovviamente maggiore rispetto ad uno scalino.
t-1 t
Fig.17.2 - Principio d’integrazione approssimata trapezoidale
Si può dunque esprimere l’integrale come yt = yt-1+ DT·(xt-1 + xt)/2
e in termini di trasformata z: y(z) = y(z) · z-1 + (DT/2) · [x(z) · z-1 +x(z)]
cioè ![]()
Uguagliando con la trasformata s ricavata precedentemente si ottiene una nuova corrispondenza, nota come trasformazione bilineare
![]()
|
|
Fig. 17.3 - Conversioni approssimate di una funzione di Laplace in funzione z , con successiva integrazione.
La Fig. 17.3 esemplifica l’applicazione di questo metodo ad una semplice costante di tempo, mostrando il confronto di precisione tra i due tipi di sostituzioni descritte.
Ovviamente nei casi di funzioni molto complesse, il calcolo dei coefficienti della funzione z generalizzata comporta notevoli elaborazioni algebriche.