Capitolo 9 ) Campionamenti asincroni

La conversione di un segnale fisico dalla forma analogica alla forma digitale richiede un sistema come in Fig. 9.1.

Il filtro anti-aliasing è opzionale, mentre il convertitore A/D (Analogico/Digitale), che normalmente è costituito da una scheda elettronica, è necessario alla trasformazione dei valori analogici istantanei y(t) (normalmente una tensione elettrica) in una serie di valori numerici y_n opportunamente codificati per essere acquisiti da un apparato elettronico digitale, quale ad esempio un calcolatore.

Fig. 9.1 - Configurazione di conversione analogico/digitale di un segnale

Il convertitore ha un suo ciclo di conversione, ha quindi una frequenza di campionamento che è asincrona rispetto al periodo del segnale in ingresso (sempre supposto periodico).

Pur continuando a supporre, per il momento, di conoscere il periodo P di y(t) e di poter predisporre la frequenza di campionamento f_c del convertitore ad un esatto multiplo della frequenza fondamentale f (=1/P) , non è possibile garantire che il primo campionamento coincida con l’inizio del periodo del segnale, come supposto sinora.

Il possibile sfasamento degli intervalli di campionamento rispetto al periodo del segnale è una nuova causa di errore nella conversione.

Se si considera infatti l’armonica f_max (precedentemente definita come la più alta armonica significativa dello spettro) campionata alla frequenza f_c = 2·f_max è semplice riscontrare che l’ampiezza rilevata dipende non soltanto dall’ampiezza effettiva dell’armonica, ma dipende in modo prevalente dallo sfasamento di f_c rispetto f_max .

Per esaminare un caso concreto, ci si può riferire all’esempio di onda triangolare della Fig. 8.4, che è la stessa analizzata nella Fig 3.3.

Si è visto in questo caso che l’armonica f_max è la quarta ( k=4 ), e ricavando dalla tabella della Fig.3.3 i coefficienti A_k (=0.0188) e B_k (=-0.0137), si può rappresentare questa armonica come in Fig. 9.2.

L’ampiezza effettiva dell’armonica corrisponde al modulo

e la sua fase iniziale (rispetto all’inizio del periodo) è q_k = atan (A_k / B_k).

La frequenza è f_max = 4 Hz, e quella di campionamento è f_c = 8 Hz.

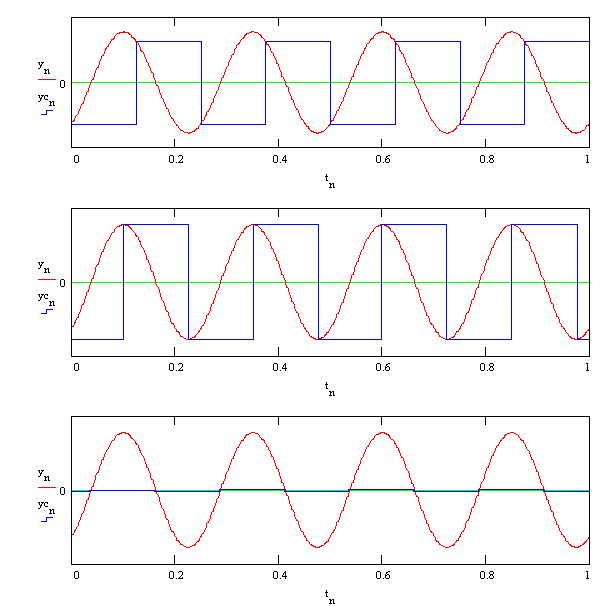
La Fig. 9.2 mostra poi tre casi di campionamento a diverso sfasamento j fra le due frequenze.

Fig. 9.2 - Effetto dello sfasamento fra armonica e campionamento nella determinazione dell’ampiezza dell’armonica stessa.

Il primo caso si riferisce al campionamento senza sfasamento, cioè con il primo rilevamento corrispondente all’inizio del periodo effettivo (la fase iniziale della quarta armonica risulta q ₄ =.994 rad @ 37 msec) e ripetizione a multipli di 250 msec.

Questa scansione darebbe un’ampiezza di .0188 (anzichè l’effettiva che è .0233).

Se però si anticipano i cicli di scansione, introducendo un certo sfasamento fra periodo e campionamento, si vede che è possibile ottenere qualsiasi ampiezza compresa fra zero ed il massimo, pur mantenendo sempre la stessa frequenza di campionamento.

In particolare si può constatare che con j = p/2 - q ₄ si ottengono campionamenti in corrispondenza dei massimi (secondo caso), e con j = - q ₄ si ottengono campionamenti in corrispondenza degli zeri (terzo caso)..

Ciò significa che, variando l’inizio del campionamento, si ha un errore nella valutazione dell’ampiezza che varia da 0 al 100%.

Trattandosi dell’ultima armonica significativa dello spettro, questo può sembrare non così importante, ma in effetti tutte le armoniche sono affette, anche se in modo minore, dall’errore d’ampiezza.

Ma, oltre all’errore d’ampiezza, tutte le armoniche del segnale convertito sono soggette anche ad un errore di fase, sempre dovuto all’intervallo DT di campionamento.

La Fig. 9.3 mostra l’effetto di sfasamento di un’armonica ad 1 Hz campionata ogni 100 msec, cioè a 10 Hz.

Lo sfasamento è in questo caso di 36° (360° / 10).

Fig. 9.3 - Effetto di sfasamemto di un’armonica dovuto all’intervallo di campionamento

Ma ancora peggiore è l’effetto di una frequenza di campionamento non multipla della frequenza del segnale.

La Fig. 9.4 rappresenta il caso di un segnale sinusoidale a 7 Hz campionato ogni 25 msec, cioè a 40 Hz.

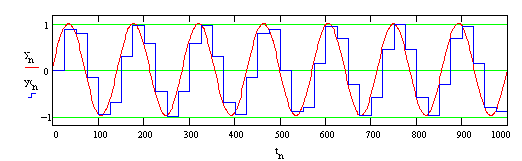
Fig. 9.4 - Effetto di un campionamento con frequenza non multipla di

quella del segnale.

Estendendo il campionamento a più cicli (7 nel caso considerato), si nota che ogni ciclo ha una diversa scansione, ciò significa che se si limitasse l’esame ad un ciclo si avrebbero campionature diverse per ognuno dei cicli.

Persino la misura del periodo (quindi della frequenza) risulterebbe diversa a seconda di quale periodo si prendesse in considerazione.

Tutte queste considerazioni pongono in risalto che la semplice osservanza del criterio di Nyquist non garantisce affatto una precisa definizione nella conversione di un segnale.

In realtà il teorema del campionamento dice solo che con la frequenza di Nyquist si possono evitare gli effetti di aliasing, ma non dice quali siano gli effetti sull’ampiezza, fase e frequenza del segnale convertito, rispetto all’originale.

Anche se spesso non evidenziati nei trattati teorici, tali errori possono però in pratica compromettere il risultato di un’applicazione concreta, ove questi non vengano correttamente valutati.

Soprattutto l’ultimo caso esaminato pone problemi sul periodo di campionamento, cioè su quanto estesa debba essere l’osservazione, oltrechè quanto fitta questa debba essere.