Capitolo 13 ) Analisi circuitali con FFT

Dopo aver visto la semplicità formale per l’uso delle FFT, è opportuno vederne subito alcune possibilità di applicazione allo studio del comportamento di circuiti elettronici.

Per tale studio sarebbe normalmente indispensabile un prototipo del cicuito ed un’adatta attrezzatura di laboratorio (multimetri, oscilloscopi, generatori di segnali, strumenti digitali, ecc.) ma, se si può esprimere matematicamente sia la forma dei segnali d’ingresso (o di ‘stimolo’, come vengono chiamati negli esperimenti), sia il comportamento dei singoli circuiti in studio, è più semplice ed immediato ricorrere al calcolo diretto dei segnali risultanti.

Questa forma di simulazione dell’esperimento ha indubbiamente il vantaggio di una grande semplicità sia formale che pratica.

Qualsiasi intervento correttivo non solo nei parametri in gioco, ma anche nelle forme dei segnali di stimolo e nella stessa struttura dei circuiti può essere ottenuto con una semplice (almeno in senso formale) intervento sui dati di calcolo.

Ovviamente ciò è merito anche dell’ambiente di sviluppo in cui si opera e sulla conoscenza dell’operatore nell’utilizzo di tali mezzi.

Il Mathcadâ è in tal senso fra i più completi e flessibili ambienti di sviluppo matematico, e le strutture di impostazione dei calcoli sono certamente fra le più intuitive. Non occorre però sottovalutare che per un suo uso corretto, anche questa forma di ‘programmazione’ deve essere studiata ed assimilata.

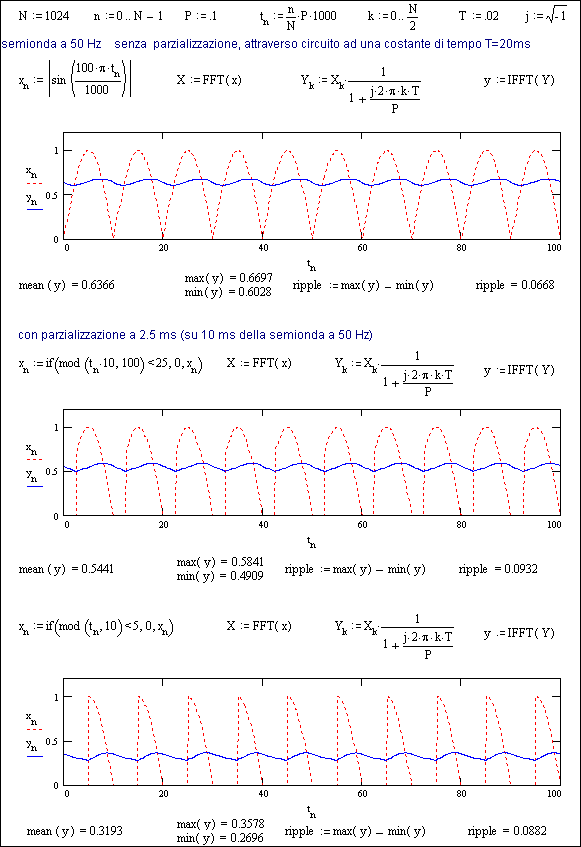
Come primo semplice esempio di simulazione di una risposta di un circuito, del tipo RC già visto nel capitolo 7, ad uno stimolo costituito da un segnale a semionda raddrizzata a 50 Hz (con o senza parzializzazione), vengono dati nella Fig. 13.1 tre diversi casi.

In ciascuno si può notare:

- la generazione di N campioni del segnale d’ingresso (x_n con n = 0...N-1 )

- la trasformazione in spettro X(f) di K frequenze (con k = 0...N/2-1)

- la moltiplicazione per la funzione di trasferimento H(f) (nell’attuale caso di una costante di tempo, quindi = 1/(1+j·w·T), con T posto uguale a 20 ms) per ottenere lo spettro Y_k  del segnale d’uscita .

- la riconversione di quest’ultimo in segnale nel tempo y_n.

Tutte queste operazioni sono svolte formalmente da una sola riga di impostazioni, immediatamente sopra il grafico che riporta l’andamento dei segnali d’ingresso e d’uscita per un tempo di 1/10 di secondo, come potrebbe essere rilevato da un oscilloscopio nel caso di reale esperimento in laboratorio.

Il calcolo è effettuato su un periodo di osservazione P di 0.1 secondi (100 ms) con 1024 campionamenti ( quindi 1 campionamento ogni circa 0.1 ms) e comprende perciò 10 semionde.

Fig. 13.1 - Esempi di analisi con FFT della risposta di circuiti a vari segnali d’ingresso (semionde a varia parzializzazione). [commento audio]

La precauzione di osservare il fenomeno su un periodo di tempo relativamente lungo non ha però fondamento, in quanto il metodo FFT fornisce direttamente risultati a regime stazionario (cioè esenti da transitori iniziali).

Il calcolo ha come scopo la determinazione del valore medio del segnale in uscita, cioè la media dei valori di y_n , e della sua ondulazione residua (ripple) in corrispondenza ai vari gradi di parzializzazione (0, 25 e 50 % rispettivamente).

Tali calcoli sono svolti immediatamente sotto i rispettivi grafici.

Come si vede, una volta impostato il calcolo ed i singoli parametri, i risultati sia grafici che numerici vengono immediatamente visualizzati, con evidenti vantaggi rispetto ad un’analoga procedura sperimentale.

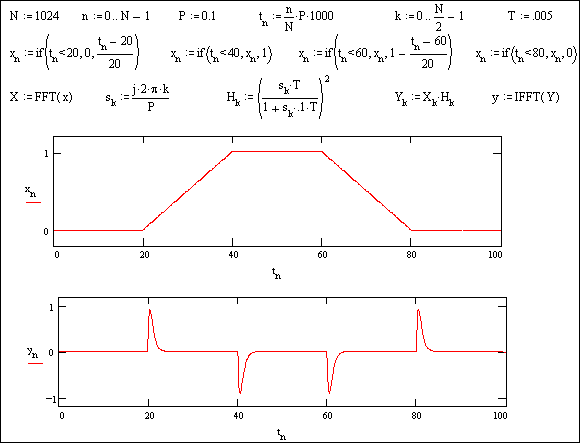
Un secondo esempio di applicazione diretta di FFT all’analisi circuitale è dato dalla Fig. 13.2, in cui viene studiato il comportamento di un circuito differenziatore di secondo ordine all’applicazione di una forma d’onda trapezoidale.

Fig. 13.2 - Altro esempio di analisi circuitale con FFT: forma d’onda trapezia attraverso un circuito derivatore di secondo ordine.

Il circuito derivatore è rappresentato dalla sua funzione di trasferimento H(s), dove s è espressione delle frequenze multiple della fondamentale (il cui periodo coincide col tempo di osservazione P), e T è la costante di derivazione.

La semplice derivazione sarebbe s ·T , ma è opportuna una limitazione alle alte frequenze con una costante di tempo distanziata di una decade. L’elevazione al quadrato rende il derivatore di secondo ordine.

Quindi x costituisce il segnale d’ingresso ed y il segnale d’uscita, ricavato calcolando lo spettro X, moltiplicandolo per la funzione di trasferimento H ed antitrasformando il prodotto Y così ottenuto.

I grafici di x e y in funzione del tempo t (in ms) sostituiscono brillantemente gli oscillogrammi che si sarebbero ricavati da una prova di laboratorio con circuiti reali

La Fig. 13.3 è infine un esempio di configurazione circuitale a caratteristiche non-lineari, facilmente simulabile mediante procedure di calcolo.

x_n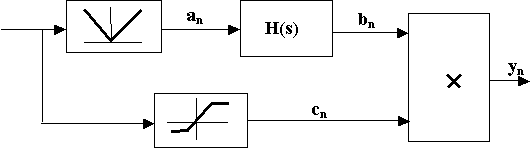

Fig.13.3 - Configurazione circuitale con caratteristiche non-lineari.

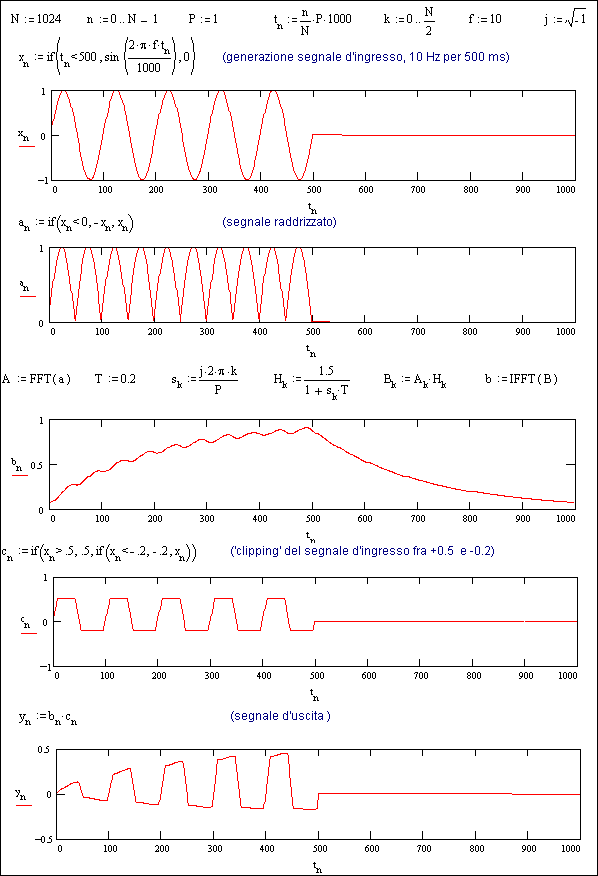
La procedura di calcolo ed i relativi risultati sono riportati in Fig. 13.4, nell’ipotesi di una forma d’onda d’ingresso costituita da un segnale sinusoidale a 10 Hz per 0.5 sec, seguito da una pausa per altri 0.5 sec.

Il periodo d’osservazione è quindi P=1 sec, mentre il tempo t_n è espresso in ms.

Come chiaramente indicato nella Fig.13.3, il circuito è composto da un blocco raddrizzatore (uscita a_n) e da una funzione di trasferimento H(s) costituita da una semplice costante di tempo con T=0.2 sec e da un fattore di amplificazione di 1.5, da cui esce il segnale b_n.

La trasformazione in frequenza di a_n consente di ottenere b_n semplicemente moltiplicando lo spettro A del segnale per la funzione di trasferimento H ed antitrasformando poi da frequenza in tempo.

Un terzo blocco limita il segnale d’ingresso x_n fra +0.5 e -0.2, generando il segnale c_n.

Il segnale d’uscita y_n è infine il prodotto fra i segnali b_n e c_n .

Anche nei casi di circuiti non-lineari (salvo ovviamente il blocco di trasferimento), il metodo di simulazione con l’uso di FFT dà quindi possibilità di facili soluzioni, senza dover ricorrere a sperimentazioni in laboratorio.

Fig. 13.4 - Esempio di analisi in una configurazione circuitale non-lineare