Capitolo 15 ) Progettazione dei filtri non-ricorsivi

Come si è visto nel capitolo precedente, il progetto di un filtro non-ricorsivo è facilmente ottenibile dall’antitrasformazione di Fourier dello spettro del filtro desiderato, ma si è anche visto che questo comporterebbe numeri di coefficienti molto elevati, quindi tempi di calcolo inaccettabili.

Volendo ad esempio utilizzare il procedimento della Fig. 14.7 per il calcolo di un filtro ‘quasi-ideale’ a 100 Hz anzichè a 10 Hz, è chiaro che si dovrebbe scegliere come massima frequenza dello spettro base almeno f_K = 512 ( K=512 se il periodo di osservazione è P=1 sec) il che comporta un numero di coefficienti (e di moltiplicazioni) N = 1024.

Si pone quindi il problema di esaminare gli effetti di una riduzione nel numero di coefficienti, fermo restando le condizioni di campionamento (cioè i valori dell’intervallo d’osservazione P , che determina il passo fra le singole frequenze dello spettro,nonchè di K ,quindi N, che in definitiva determinano l’intervallo di campionamento DT = P/N).

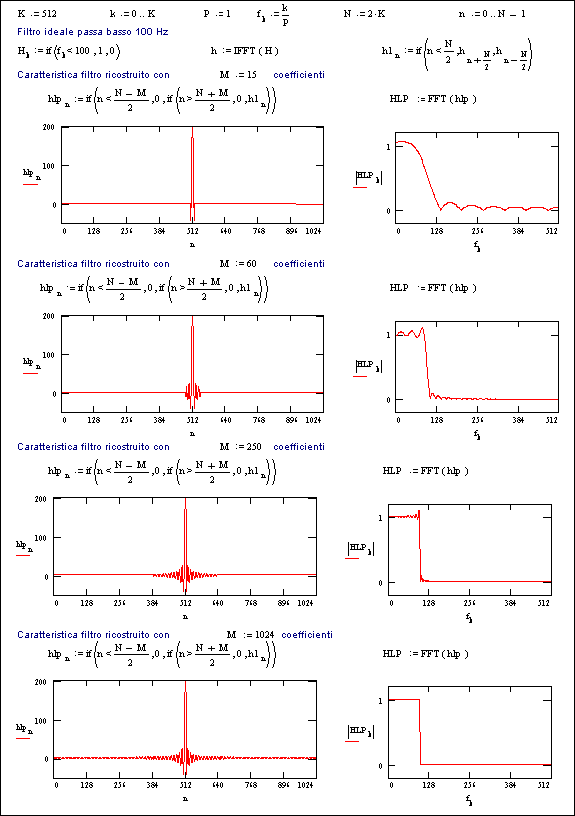
La Fig. 15.1 mostra tali effetti su un filtro passa-basso a 100 Hz.

In tale figura si crea uno spettro rettangolare H (ampiezza 1 per tutte le frequenze <100 Hz e 0 per quelle >100 Hz) e si ricavano i coefficienti h con l’antitrasformazione IFFT .

Considerando uno spettro di 512 frequenze si ottengono 1024 coefficienti (in realtà solo 512 sono significativi e gli altri sono speculari). Per meglio mostrare tale specularità, si è proceduto alla traslazione dello spettro (h1, riferito allo zero, cioè fra -N/2 e +N/2 o, indifferentemente, riferito a N/2, fra 0 e N).

Se per la ricostruzione del filtro si utilizza solo una parte M dei coefficienti (si effettua cioè un troncamento, ponendo a zero i coefficienti esterni al tratto -M/2 e +M/2) si ottiene una caratteristica meno netta e che presenta oscillazioni (ringing) del segnale d’uscita. Queste sono note nella letteratura tecnica come oscillazioni di Gibbs e sono duali nella frequenza a quelle che si rilevano ricostruendo un impulso rettangolare nel tempo con un troncamento di frequenze dello spettro.

Si può anche vedere questo fatto come risultato della convoluzione in frequenza della funzione di trasferimento ideale con la trasformazione dell’intervallo rettangolare nel tempo (quindi del tipo sen(x)/x ), equivalente agli M coefficienti effettivamente considerati .

Nell’esempio in Fig. 15.1, avendo assunto K=512 e P=1 sec, si ha N=1024, Df =1 Hz e DT@0.977 ms.

La ricostruzione della caratteristica del filtro (spettro di frequenza) risultante dal troncamento si ottiene ovviamente con la trasformazione FFT della serie ridotta degli M coefficienti.

La figura mostra graficamente sia l’andamento dei coefficienti, sia la caratteristica del filtro nei casi di M=15, =60, =250 e =1024, per evidenzare la diversa influenza delle oscillazioni di Gibbs e la diversa ‘pendenza’ della transizione fra frequenze passanti e frequenze bloccate.

Ovviamente l’ultimo caso rappresenta il filtro ‘quasi-ideale’.

Fig. 15.1 - Calcolo dei coefficienti di un filtro ideale passa-basso e sua ricostruzione con troncamento nel numero dei coefficienti.

Le oscillazioni di Gibbs rilevate nei casi di troncamento possono essere attenuate con l’utilizzo di forme di finestre come quelle viste al capitolo 11.

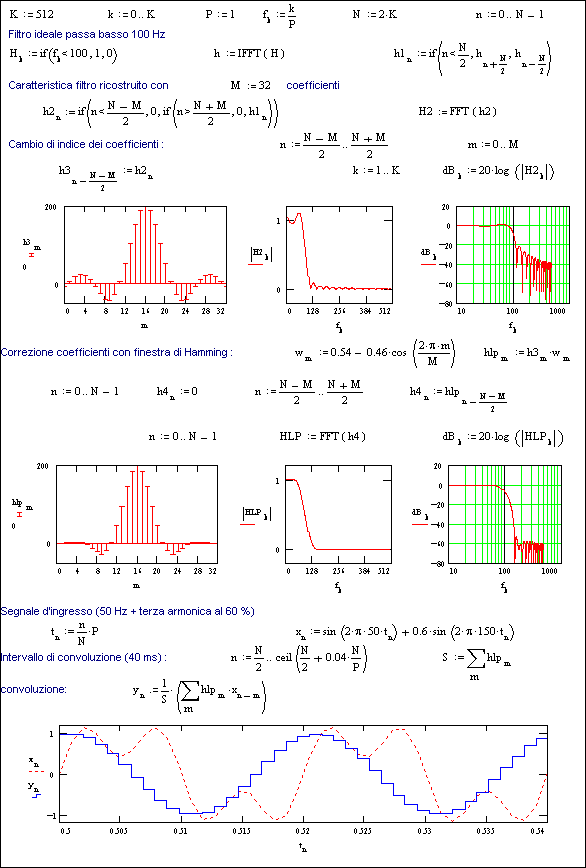
La Fig. 15.2 illustra infatti una possibile procedura di progetto di questo tipo di filtro, passa-basso a 100 Hz, con 32 coefficienti (invece che 1024) e l’utilizzo di una finestra di Hamming per lo smorzamnento delle oscillazioni nella caratteristica in frequenza.

Per maggior chiarezza, oltre agli spettri in frequenza del filtro senza e con smorzamento, vengono indicati anche i relativi diagrammi di Bode, cioè in scale logaritmiche, che mettono meglio in risalto il diverso effetto di attenuazione delle alte frequenze.

A dimostrazione dell’effetto di filtraggio risultante, la figura riporta anche il caso ormai più volte utilizzato (Fig. 1.2 e Fig. 6.2) di un segnale sinusoidale a 50 Hz con terza armonica applicato come ingresso al filtro.

Il segnale d’uscita risulta pertanto la convoluzione dei coefficienti hlp (low-pass) del filtro prima calcolati con i singoli campionamenti x del segnale d’ingresso.

L’ultimo grafico di tale figura riporta sia questo segnale d’ingresso (a tratti) sia quello d’uscita (a gradini) dal filtro, che ovviamente è la sola sinusoide a 50 Hz.

A chiarimento della procedura seguita se ne evidenziano alcuni aspetti:

- dopo aver definito la caratteristica ideale H, si ricavano i coefficienti h del filtro quasi-ideale. Avendo scelto K=512 il numero di questi è N=1024, come già detto.

- riferendo i coefficienti a N/2 si ricava la nuova serie h1

- scegliendo M (=32) si devono azzerare tutti i coefficienti fra 0 ed (N-M)/2 nonchè quelli fra (N+M)/2 ed N-1, ottenendone la serie h2. Da questa si può ricavare la nuova caratteristica del filtro H2.

- riferendo i coefficienti all’indice m = 0....M si ottiene la serie h3. Si noti che in realtà il numero dei coefficienti diventa M+1, per rispettare la simmetria rispetto al valore centrale.

- a questa serie viene applicata la finestra di Hamming, ottenendo finalmente la serie dei coefficienti hlp.

- per ottenere la caratteristica finale del filtro HLP, occorre però ricostruire la serie completa di N valori, cioè h4. L’effetto di smorzamento sui coefficienti laterali e di conseguenza nello spettro (che non presenta più oscillazioni) è evidente nei rispettivi grafici.

- per la prova del filtro si genera una sinusoide a 50 Hz con terza armonica (x) e si esegue una convoluzione con i coefficienti di questo.

- per ridurre al minimo il tempo richiesto nella simulazione al calcolo della convoluzione, si limita questa ad un intervallo temporale di 40 ms, il che equivale a due cicli del segnale d’ingresso. L’inizio della convoluzione si è posto alla metà del periodo P, il che permette la scelta di M sino ad un massimo di N/2 coefficienti.

Fig. 15.2 - Progetto di un filtro passa-basso a 100 Hz con 32 coefficienti e sua applicazione ad un segnale a 50 Hz con terza armonica.

- i singoli valori del segnale d’uscita y sono il risultato della convoluzione, divisa per la somma S dei coefficienti.

Il segnale d’uscita che appare nell’ultimo grafico presenta uno notevole sfasamento rispetto al segnale d’ingresso: è questo l’effetto della convoluzione che comporta un ritardo pari alla metà del tempo corrispondente all’acquisizione degli M valori di campionamento.

Tale tempo è quindi (M/2)·DT , cioè (M/2)·P/N , ed è un tempo fisso che incide perciò sullo sfasamento di ogni singola frequenza in modo proporzionale al singolo valore.

Nel caso dell’esempio di Fig. 15.2 questo tempo assume un valore di circa 16 ms, quindi per la sinusoide a 50 Hz, con un periodo di 20 ms, lo sfasamento equivale ad 8/10 di 360°, cioè 288°.

Va evidenziato che la procedura di progetto della Fig. 15.2 è del tutto generale per i filtri passa-basso, il che significa che, disponendo del Mathcadâ è possibile utilizzarla per il progetto di qualsiasi filtro passa-basso, purchè vengano opportunamente impostati i parametri relativi.

Va tuttavia segnalato che la procedura indicata, pur essendo valida per la progettazione, è più adatta a scopi didattici che a progetti veramente professionali. Il motivo è che la sua applicazione pratica richiede una serie di tentativi per la ricerca dei parametri che risolvano al meglio il problema, mentre esistono programmi di progettazione al calcolatore che ricavano direttamente le soluzioni ottime.

Naturalmente ciò richiede la disponibilità di tali programmi e generalmente anche ambienti di sviluppo molto sofisticati.

Con tale premessa, vengono presentate qui di seguito le analoghe procedure per il calcolo degli altri tipi di filtri.

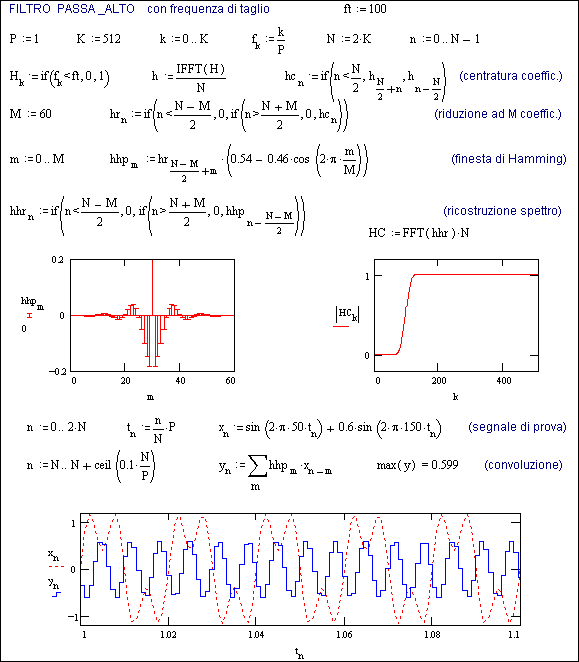
La Fig. 15.3 costituisce una procedura di progetto di filtro passa-alto.

Nell’esempio vengono ricavati gli M coefficienti hhp (high-pass) del filtro per la convoluzione con il segnale d’ingresso.

Dopo aver fissato la caratteristica del filtro quasi-ideale H, si ricavano con l’antitrasformazione IFFT i coefficienti h, che vengono poi centrati rispetto alla metà del periodo (hc).

Stabilito il numero di coefficienti da considerare (M=60) si estraggono i coefficienti centrali, moltiplicati per i termini della finestra di Hamming, ottenendo i coefficienti cercati hhp.

Per ricostruire lo spettro di frequenze effettivo occorre azzerare i coefficienti fra 0 e (M-N)/2 nonchè fra (M+N)/2 e N-1 ed infine trasformare con FFT .

Lo spettro risulta privo di oscillazioni grazie appunto all’uso della finestra di Hamming.

La figura è completata dall’ esempio della solita forma d’onda a 50 Hz con terza armonica. La convoluzione fra i coefficienti hhp ed i campionamenti x , limitata a 0.1 sec per ridurre il tempo di calcolo, produce il segnale y d’uscita dal filtro che ovviamente è la sola terza armonica a 150 Hz. Il grafico a gradini mette in risalto il campionamento ogni DT = P/N @ 0.976 ms.

Fig. 15.3 - Progetto di filtro non-ricorsivo passa-alto

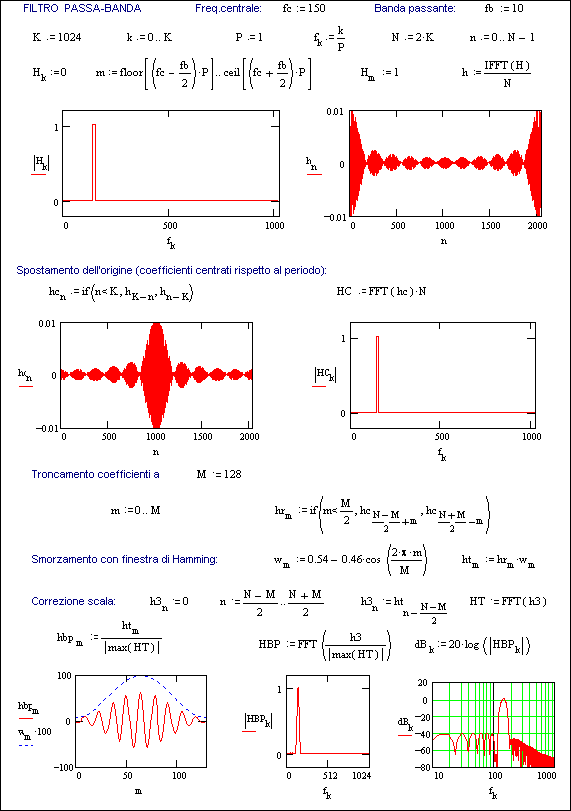
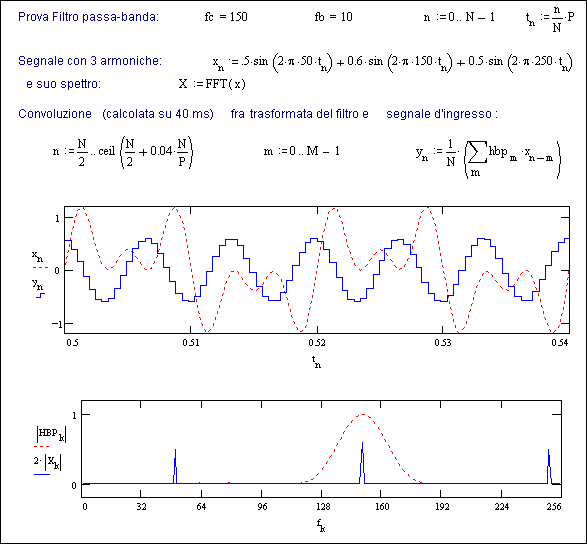
Similmente, la Fig. 15.4 rappresenta una procedura di progetto per un filtro passa-banda.

Volendo mantenere l’applicazione nel campo delle frequenze industriali fino alla quinta armonica, occorre maggiorare in questo caso la definizione e perciò si è previsto K = 1024 il che, lasciando invariato P = 1 sec, comporta un campionamento di N = 2048 punti, cioè un campionamento ogni circa mezzo millisecondo.

Fig. 15.4a - Progetto di filtro non-ricorsivo passa-banda.

Anche il mumero di coefficienti M utilizzati per la convoluzione è stato elevato a 128. Malgrado ciò, il comportamento del filtro, che è illustrato nella Fig. 15.4b, è evidentemente approssimato, anche se risponde pienamente allo scopo di estrarre la sola terza armonica da un segnale d’ingresso x a 50 Hz con terza e quinta armonica

La linea tratteggiata dell’ultimo diagramma rappresenta infatti lo spettro passante del filtro che, come si vede, lascia inalterata la sola terza armonica (150 Hz) azzerando invece sia la fondamentale (50 Hz) che la quinta (250 Hz).

Fig. 15.4b - Verifica del filtro passa-banda progettato in Fig.15.4a.

Non viene dato un esempio di progetto per il filtro arresta-banda (band-stop), data l’ovvietà della procedura, potendosi sommare gli effetti di un passa-alto e di un passa-basso.