Capitolo 16 ) Strutture ricorsive

Nell’introdurre i filtri numerici (capitolo 14) si è constatato che una costante di tempo rappresenta la forma più semplice di filtraggio passa-basso di un segnale.

Riprendendo in considerazione quanto detto a proposito del circuito RC (capitolo 7) che è appunto una tipica costante di tempo, si ha che l’equazione che lega l’andamento dei segnali v d’ingresso e vc d’uscita con i parametri caratteristici del circuito, R e C, è:

Se ora, invece di applicare le trasformazioni di Laplace come è stato fatto al capitolo 7, si risolve questa equazione differenziale col metodo delle differenze finite, cioè con intervalli di tempo finiti anzichè infinitesimi, si ottiene:

dove vc_t è la tensione d’uscita all’istante t , mentre vc_t-1 è la tensione all’istante t - Dt , con Dt intervallo di campionamento.

Questo permette di ottenere, indicando con T = R·C la costante di tempo,

e di risolvere quindi l’equazione differenziale di partenza con operazioni puramente aritmetiche. Ovviamente la soluzione è approssimata e si avvicina sempre più a quella esatta nella misura in cui Dt tende a zero.

La struttura di calcolo relativa a questa soluzione può essere rappresentata come in Fig. 16.1, indicando con x e y i segnali rispettivamente d’ingresso e d’uscita, e con a e b le costanti moltiplicative (espressioni fra parentesi).

Si noti che per il caso della costante di tempo è a + b = 1.

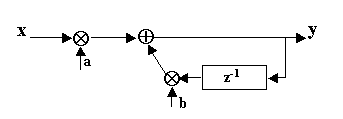
Fig. 16.1 - Struttura di calcolo di una costante di tempo.

Il blocco indicato con z^-1 è un ritardo di tempo di durata Dt sec, che fornisce in uscita all’istante t il valore che si era presentato al suo ingresso all’istante precedente t-Dt.

La notazione z^-1 fa riferimento ad una particolare forma di trasformate, note come trasformate z , simili a quelle di Laplace, ma valide essenzialmente per segnali discreti, quindi adatta proprio agli apparati digitali.

La trasformazione di una funzione discreta f(n), campionata ogni Dt. quindi in cui t = n·Dt. (con n da 0 ad ¥), e con f(n)=0 per tutti i valori di n<0, è

mentre l’antitrasformata è

Per l’uso di queste trasformazioni si rimanda alle appendici.

Per ora è importante notare che la struttura di calcolo presenta una forma di retroazione del segnale d’uscita, che quindi influisce sulla sua stessa formazione.

Ciò comporta un certo mantenimento del segnale in uscita, teoricamente all’infinito, anche se viene a mancare il segnale d’ingresso.

Per tale caratteristica le strutture di questo tipo vengono chiamate oltre che ricorsive, anche IIR (Infinite Impulse Response).

Interpretando il significato fisico dei coefficienti nella struttura di Fig.16.1, si può dire che b rappresenta il decadimento naturale del segnale d’uscita. infatti in assenza del segnale d’ingresso (x=0) l’uscita y (supposto che abbia già raggiunto un valore ¹0) decade con bⁿ (essendo b<1, y tende a 0 per n®¥).

Il coefficiente a rappresenta invece il fattore d’incremento che il segnale d’ingresso provoca ogni Dt su quello d’uscita.

Inoltre è interessante notare che la stessa struttura è più generale della sola costante di tempo: infatti se i coefficienti a e b non sono fra loro complementari ad 1, si possono avere comportamenti diversi da quanto visto.

In particolare se b = 1, cioè non vi è decadimento naturale del segnale d’uscita, il sistema diventa un integratore, con a come costante d’integrazione.

In questo caso, se il segnale d’ingresso è un gradino di valore x , si ha un’uscita y crescente linearmente con pendenza x·a/Dt.

Ma la struttura può essere ampliata con più stadi di ritardo nella retroazione, quindi con diversi coefficienti b₁ , b₂ ..... b_p ed inoltre è possibile aggiungere anche stadi di ritardo al segnale d’ingresso, esattamente come nelle strutture non-ricorsive, con coefficienti a₀ , a₁ ..... a_q.

La Fig. 16.2 rappresenta il caso più generale di una struttura di questo tipo, in cui i numeri di coefficienti p e q , rispettivamente nel numeratore e nel denominatore della funzione in z, ed i valori dei singoli coefficienti stabiliscono il comportamento del blocco, cioè come questo trasforma il segnale d’ingresso x in segnale d’uscita y.

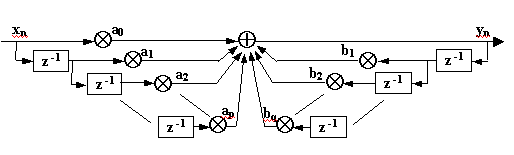
Fig. 16.2 - Struttura generalizzata della funzione H(z).

La funzione di trasferimento in z è quindi espressa da:

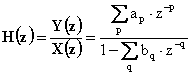
con p da 0 al massimo numero di ritardi del segnale d’ingresso e q da 1 al massimo numero di ritardi del segnale d’uscita.

Ciò permette una semplice svolgimento del calcolo nel dominio del tempo con i p campioni del segnale d’ingresso ed i q campioni del segnale d’uscita e ricavati negli istanti precedenti t, moltiplicati per i rispettivi coefficienti:

y_t = a₀·x_t + a₁·x_t-1 + a₂·x_t-2 + ....... +b₁·y_t-1 + b₂·y_t-2 + ........

Questo è un importantissimo metodo, che permette di esprimere, sia pure in forma approssimata, il comportamento di qualsiasi sistema di trasferimento.

Infatti tale struttura non riguarda solo i filtri veri e propri, ma il concetto può essere esteso a qualsivoglia blocco che elabora un segnale per generarne un altro.

Certamente il problema pratico è quello di determinare il numero degli stadi e soprattutto i valori dei coefficienti necessari ad esprimere un certo comportamento e gran parte del seguito sarà quindi dedicato ai metodi di ricerca di tali valori, cioè in definitiva al tentativo di ricavare dei modelli numerici dei blocchi più significativi.

Data la sempre maggior importanza della simulazione numerica nello studio di apparati industriali, verranno nel seguito anche illustrate le procedure di impiego di tali modelli, soprattutto in apparati di regolazione automatica.