Capitolo 19) Predeterminazione risposta di un blocco
La possibilità di realizzare filtri molto selettivi vista nel capitolo precedente, apre grandi prospettive nella realizzazione di funzioni di trasferimento ad andamento predeterminato.
Unendo l’azione di più filtri accordati su diverse frequenze di risonanza e con guadagni prefissati è in linea di principio costruibile qualsiasi forma desiderata di spettro di frequenze, quindi di ‘risposta’ della funzione di trasferimento.
Si è infatti visto che lo spettro di frequenza stesso non è altro che una sequenza di valori discreti di guadagni alle singole frequenze, distanziate fra loro di 1/T, quindi si può pensare di approssimare questo andamento con un certo numero di blocchi passa-banda adiacenti, purchè la banda sia sufficientemente stretta ed i guadagni fuori dalla banda siano trascurabili.
Ove i tempi di elaborazione lo permettano, è perfino possibile utilizzare un solo blocco biquadratico per rilevare la composizione in frequenza di un segnale, cioè l’equivalente approssimata dell’analisi di Fourier, memorizzando prima gli N campioni del segnale d’ingresso nel tempo di osservazione T ed applicando poi in successione e ripetitivamente tali campioni al blocco, cambiando di volta in volta i parametri per individuare l’ampiezza relativa a ciascuna banda.
Tale disposizione è utilizzata in particolare nello studio di forme d’onda acustiche, per rilevare le componenti dei suoni, sia vocali che strumentali.
Più comune è tuttavia disporre in parallelo blocchi diversamente accordati e utilizzare l’insieme per modificare opportunamente, secondo criteri stabiliti, il segnale applicato all’ingresso.
Le applicazioni più evidenti sono i filtri con caratteristiche particolarmente elevate e comunque rigorosamente prefissate. Appositi programmi di calcolo sono stati sviluppati per ottimizzare queste applicazioni ed alcuni esempi sono riportati in appendice.
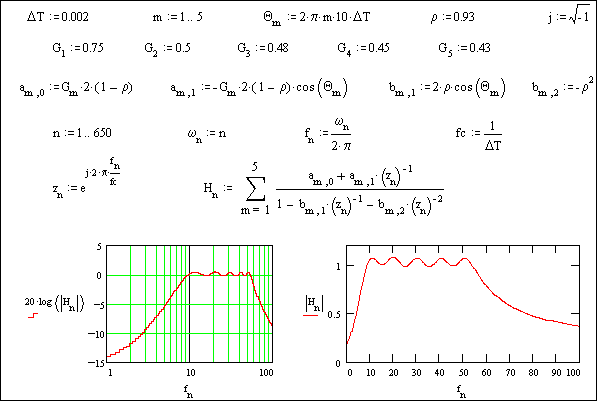
Per una miglior comprensione di queste possibilità, la Fig. 20.1 mostra l’effetto della messa in parallelo di 5 filtri a risonanza (del tipo illustrato nella Fig. 19.7), per ottenere un filtro passa-banda a caratteristica quasi piatta fra 10 e 50 Hz.
Si sottolinea che l’esempio è una semplice dimostrazione del metodo e non rappresenta un’ottimizzazione. I guadagni fissati per ciascuna banda compensano in realtà la somma degli effetti collaterali degli altri blocchi.
Si comprende tuttavia che prefissando opportunamente i singoli guadagni ed ovviamente il numero di blocchi in parallelo, sia possibile ottenere qualsiasi andamento prefissato, come sopra detto.
Va citato che questo potrebbe essere utilizzato per costruire un modello di una reale funzione di trasferimento rilevata ad esempio sperimentalmente su una macchina o su un impianto.
|
|
Fig. 20.1 - Esempio di utilizzazione in parallelo di blocchi biquadratici risonanti.
Con tale modello, realizzato con hardware dedicato oppure semplicemente con un programma in un calcolatore (se sufficientemente veloce da permettere la simulazione in tempo reale), sarebbe possibile lo studio sperimentale ed una messa a punto di anelli di regolazione automatica completamente fuori linea, cioè senza effettivamente impegnare la macchina o l’impianto, con evidenti vantaggi di flessibilità e sicurezza.
Tale argomento, estremamente importante fra le applicazioni industriali della tecnica dei segnali numerici, verrà ripreso più avanti nei capitoli dedicati al controllo.
Fra le funzioni a comportamento predeterminato vanno annoverati anche gli oscillatori, cioè blocchi biquadratici tarati per oscillare permanentemente ad una frequenza stabilita.
Nel capitolo precedente si è visto che la condizione limite di stabilità si ha con poli di modulo unitario.
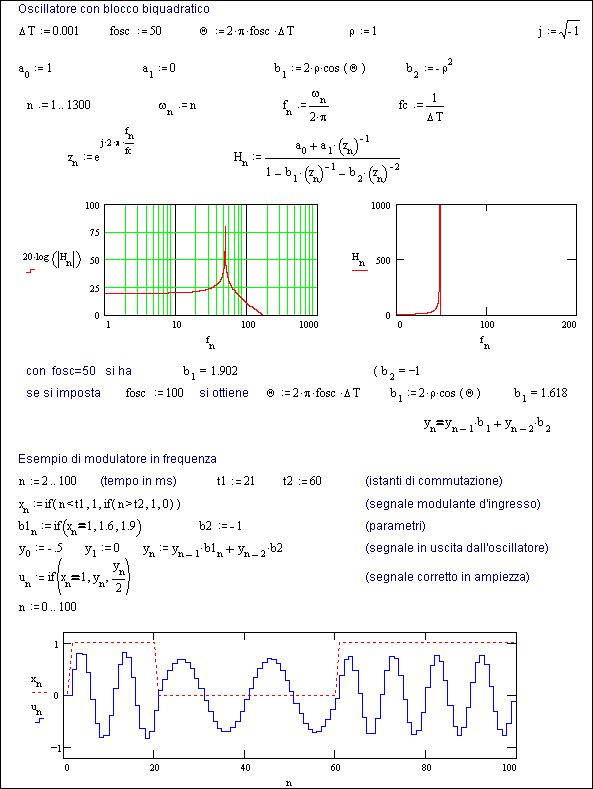
Sfruttando tale caratteristica possiamo impostare i parametri di un blocco biquadratico con i valori rz=0 (a1=0 e a2=0) e al numeratore rp=1 e Qp=2·p· fosc·DT (b1=2·cos(Qp) e b2=-1), dove fosc è la frequenza (in Hz) a cui si vuole far oscillare il blocco.
La corrispondente equazione nel tempo è semplicemente yt = xt+ yt-1·b1 + yt-2· b2 .
Nel caso di blocco biquadratico in hardware è sufficiente un segnale d’ingresso impulsivo iniziale per innescare l’oscillazione, ma nel caso di implementazione in software si può anche ignorare l’ingresso predisponendo il valore iniziale y0 ad un valore diverso da zero (tale valore determina l’ampiezza dell’oscillazione).
Si fa notare che la frequenza di oscillazione dipende unicamente dal parametro b1 e che questa cambia quando si cambia tale parametro. Questo permette non solo di stabilirla inizialmente, ma anche di modularla nel tempo quando l’oscillazione è in corso.
La Fig. 20.2 fornisce un esempio di oscillatore realizzato con un blocco biquadratico e modulato poi in frequenza.
I diagrammi di Hn dimostrano la risonanza, teoricamente infinita perchè coincidente col polo, in corrispondenza della frequenza di oscillazione (fosc) impostata.
Il blocco, una volta eccitato con un impulso d’ingresso o in modo equivalente con un segnale iniziale d’uscita non nullo, entra pertanto in oscillazione praticamente permanente.
In particolare l’esempio si riferisce al caso di un generatore a 2 toni, tipico nella trasmissione telegrafica a modulazione in frequenza.
Se questo fosse realizzato in hardware sarebbe sufficiente commutare i valori di b1 per trasmettere i segnali di 0 e 1 dei codici binari dei vari caratteri, mentre nella simulazione in figura si è programmata tale modulazione in funzione del tempo (xn è utilizzato unicamente per rappresentare graficamente tale modulazione) e si è corretta inoltre la differenza di ampiezza derivante dal cambiamento di frequenza.[1])
Il principio di variazione cosiddetta dinamica dei parametri, cioè il loro cambiamento nel tempo, è di importanza fondamentale nella tecnica della elaborazione numerica dei segnali.
Tale variazione consente infatti di adottare di volta in volta comportamenti diversi dell’intero blocco di trasferimento, quindi di ottenere in uscita risposte diverse rispetto al segnale d’ingresso.
Generalizzando questo caso, possiamo idealmente pensare di generare qualsiasi forma d’onda in uscita purchè venga applicato all’ingresso un segnale che contenga tutto lo spettro di frequenze che serve per definire il segnale stesso.
Il segnale d’ingresso ideale è l’impulso unitario d o di Dirac, che come visto contiene uno spettro uniforme di tutte le frequenze. In pratica potremo avvicinarci a questo con impulsi sufficientemente stretti, ma di grande ampiezza.
Questa possibilità verrà più ampiamente illustrata nel capitolo dedicato alla generazione di suoni sintetizzati.
|
|
Fig. 20.2 - Oscillatore ricavato da un blocco biquadratico, sua implementazione nel tempo ed esempio di modulatore a 2 toni.
Altra importante applicazione derivante dalla possibilità di variazione dinamica dei parametri è l’ottimizzazione dei controlli automatici numerici.
Se il blocco considerato è la parte di regolazione di un anello chiuso, quindi i suoi parametri definiscono il comportamento del regolatore, è evidente che qualsiasi criterio di ottimizzazione può condizionare nel modo più opportuno la variazione dei parametri e quindi la risposta dell’anello di regolazione.
Anche questo argomento verrà ampliato più avanti, nel capitolo dedicato all’ottimizzazione dei controlli automatici.
Se invece il blocco considerato riguarda la simulazione del sistema sotto controllo, sempre nell’anello chiuso di regolazione, la variazione dinamica dei parametri consente una simulazione più realistica del sistema stesso, potendo riprodurre nel tempo variazioni, programmate o casuali, delle possibili variazioni di comportamento del sistema in esame.
Esempi di queste possibilità verranno illustrati nel capitolo della simulazione dei sistemi automatici.