Capitolo 25 ) Configurazioni antisaturazione

Per ridurre gli effetti della saturazione negli anelli di regolazione si possono adottare speciali configurazioni di controllo.

Nel caso di sistemi a parametri costanti nel tempo (che ad esempio non presentino brusche variazioni di carico o ampi disturbi), il sistema più semplice è quello di interporre fra il segnale di riferimento e l’ingresso al regolatore un circuito a rampa, cioè un circuito limitatore della massima variazione del segnale nel tempo.

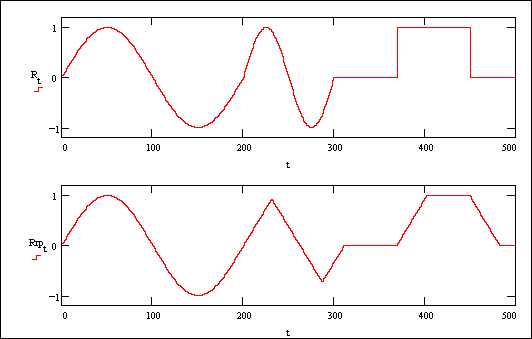
La Fig. 25.1 mostra l’effetto di un tale circuito: quando al suo ingresso è applicato un segnale R (primo grafico), l’uscita risulta Rrp (secondo grafico), e cioè uguale ad R solo se questo varia lentamente altrimenti si ha un andamento lineare..

Fig. 25.1 - Effetto dell’applicazione di un circuito a rampa sul segnale di riferimento R.

In effetti il circuito a rampa stabilisce la massima ‘pendenza’ del segnale di riferimento, in modo che l’errore della grandezza controllata risulti sempre abbastanza piccolo e che quindi si eviti la saturazione nell’uscita del regolatore.

Questo ovviamente riduce la dinamica del sistema e la pendenza della rampa dovrebbe essere fatta corrispondere alla massima variazione ‘naturale’ (senza alcun forzamento) del sistema stesso, cioè alla sua principale costante di tempo.

Nei sistemi digitali la rampa è in realtà un andamento a gradini, ciascuno dei quali ha durata DT (intervallo di campionamento) e altezza DR (massima variazione ammessa).

Se il controllo è implementato a programma, una possibile procedura (in linguaggio Basic) è indicata nella Fig. 25.2, in cui le variabili hanno il significato già visto.

Naturalmente tale procedura deve essere eseguita ad ogni DT.

If Rrp < R - DR Then

Rrp = Rrp + DR

ElseIf Rrp > R + DR Then

Rrp = Rrp - DR

Else

Rrp = R

End If

Fig. 25.2 - Programma Basic per la realizzazione di una rampa.

Nel caso di un sistema con una costante di tempo T , con un valore massimo di riferimento Rmax e con intervallo di scansione DT, il gradino DR dovrebbe quindi essere posto uguale a Rmax· DT / T.

Questo evita il pericolo di sovraelongazioni (superamento del riferimento) nei casi in cui ciò è indesiderato, come ad esempio nei controlli di posizione.

Una soluzione più sofisticata è la struttura anti-windup, che deriva il suo nome dal termine inglese windup, cioè dall’azione di accumulo di controllo dovuta alla parte integratrice del regolatore, durante le fasi di saturazione del segnale in uscita dal regolatore stesso.

Quando il regolatore è saturato infatti, il sistema riceve un segnale fisso, non più dipendente dall’errore, mentre l’integratore continua ad accumulare l’errore ben oltre il valore strettamente necessario a mantenere l’equilibrio una volta raggiunto l’errore nullo. Ciò comporta quindi una conseguente sovraelongazione, fino a che la parte proporzionale (di segno opposto) e l’integrazione dell’errore (pure questo di segno opposto) non hanno annullato tale accumulo.

Nei regolatori analogici la struttura anti-windup classica prevede un integratore della differenza fra segnale di correzione (u) e l’effettivo segnale d’uscita (usat). Se questo integratore ha la stessa costante di quello del regolatore e la sua uscita viene sottratta alla somma dell’azione regolatrice (vedi Fig. 25.3), l’effetto di accumulo viene evitato.

Nei sistemi digitali è più semplice bloccare l’azione integratrice del regolatore quando si verifica la saturazione. In effetti non occorre nemmeno rilevare usat, in quanto è possibile confrontare direttamente u con i limiti noti dell’uscita e permettere le successive integrazioni solo quando u risulta entro questi limiti.

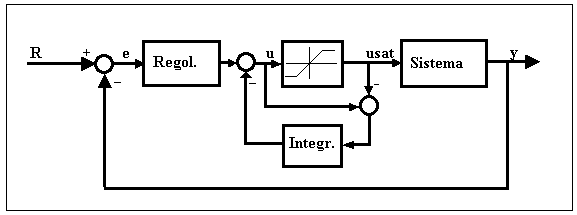
Fig. 25.3 - Struttura anti-windup classica per sistemi analogici.

La flessibilità dei sistemi digitali permette però anche altre più raffinate soluzioni, quali i regolatori a struttura variabile (VS-PI).

L’osservazione che l’azione integratrice serve solo quando l’errore diventa piccolo e che l’azione proporzionale tende a saturare l’uscita quando l’errore è grande, suggerisce di far dipendere i parametri del regolatore dall’entità dell’errore stesso.

Gli algoritmi più opportuni per tali strutture sono ancora in fase di studio, ma il concetto fondamentale è quello di far dipendere il guadagno proporzionale all’inverso del valore assoluto dell’errore e la costante integrativa dall’inverso del suo quadrato.

Kp₀ Ki₀

Kp = Ki =

1 + cp·çe ç 1 + ci·e²

In tal modo, con una opportuna scelta dei parametri iniziali Kp₀ e Ki₀ e dei coefficienti cp e ci, è possibile migliorare il comportamento dinamico dell’anello chiuso anche in presenza della saturazione.

Le Fig. 25.5a...d mostrano le risposte ottenute con regolatori diversi sul medesimo sistema, ma è opportuno premettere un’analisi più approfondita sull’azione dei parametri.

Con un classico regolatore PI , come visto al capitolo 21, la funzione di trasferimento è

R(s) = Kp + Ki / s

che nella versione digitale (capitolo 22) si trasforma in

R(z) = (ar₀ + ar₁·z^-1) / (1 - br₁·z^-1)

I parametri del regolatore digitale possono essere espressi in funzione dei guadagni proporzionale (Kp) e integrale (Ki) con le relazioni:

ar₀ = Ki·DT + Kp ar₁ = - Kp br₁ = 1

Si è anche visto (Fig. 22.2) che se il sistema controllato ha una sola costante di tempo T e se non vi è saturazione, può essere prefissata la costante di tempo Tdes dell’anello chiuso.

Ma in presenza di saturazione (Fig. 21.6) l’uscita del regolatore ha un valore costante umax e la grandezza regolata y segue semplicemente la legge esponenziale (risposta al gradino, almeno finchè dura lo stato di saturazione).

Per un’analisi più approfondita del fenomeno è opportuno considerare l’effetto separato delle azioni proporzionale ed integrale.

La Fig. 25.4 indica due schemi di calcolo, diversi ma equivalenti, per implementare un regolatore PI numerico: il primo fa riferimento alle relazioni polinomiali precedentemente citate, mentre il secondo è ricavato direttamente come somma della pura azione proporzionale e della pura azione integrale, cioè

up_t = Kp · e_t ui_t = ui_t-1 + Ki · e_t u_t = up_t + ui_t

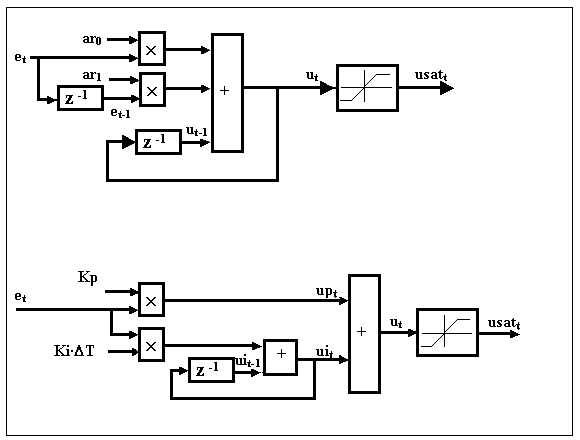
Fig. 25.4 - Strutture di calcolo equivalenti per l’implementazione di un regolatore numerico di tipo PI.

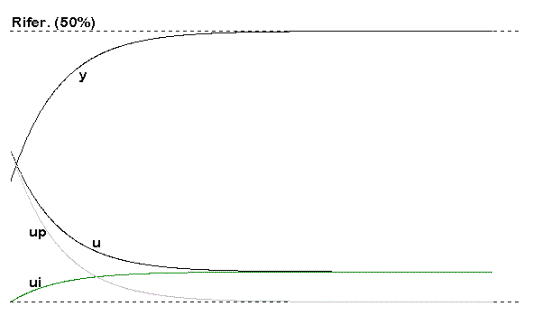
La Fig. 25.5a mostra la risposta di un sistema ad una costante di tempo, controllato da un regolatore PI con uscita non saturata. Nella parte inferiore vengono indicati gli andamenti separati delle azioni proporzionale (up) e di quella integrale (ui), nonchè il loro totale, cioè l’uscita u del regolatore.

La risposta risultante segue quindi la teoria e i parametri Kp e Ki sono stati ottimizzati per ottenere una costante di tempo prefissata (Tdes).

Fig. 25.5a - Risposta di un sistema senza saturazione.

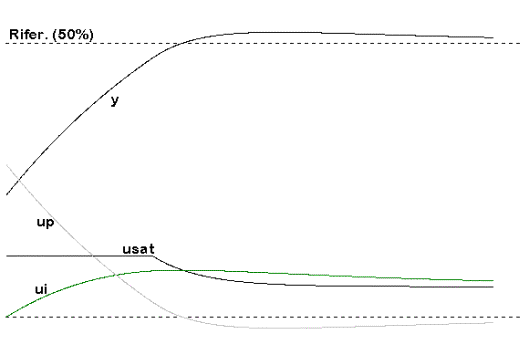
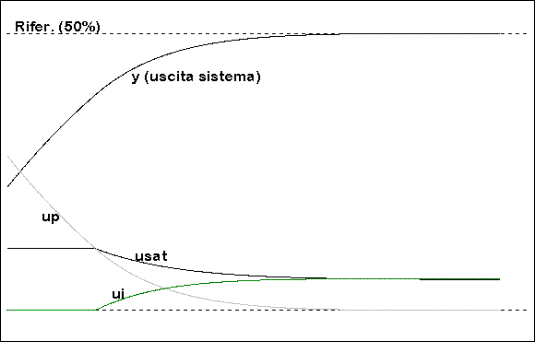
Fig. 25.5b - Risposta di un sistema in presenza di saturazione.

Ma se nelle stesse condizioni si considera la saturazione, l’andamento della risposta si modifica come rappresentato in Fig. 25.5b: in questo caso l’uscita non è più u, ma è usat, cioè se la somma u supera un dato limite questa viene bloccata a quel limite e l’effetto è quindi la risposta naturale del sistema al massimo gradino, indipendentemente dal valore del riferimento. Se questo non è il massimo (nell’esempio è stato considerato il 50% del massimo) si può avere una sovraelongazione che viene esaltata finchè ui non rientra al suo valore di regime (errore e=0, quindi up=0).

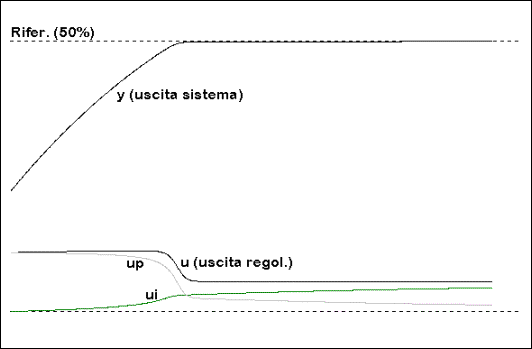
Fig. 25.5c - Risposta di un sistema con anti-windup.

Una disposizione anti-windup evita, come si è detto, che l’integrazione abbia luogo durante la saturazione, quindi evita la sovraelongazione, ma allunga ovviamente il tempo occorrente per entrare in una data banda di tolleranza (errore assoluto inferiore ad una soglia prefissata).

Nei sistemi numerici è semplice realizzare un dispositivo anti-windup, ponendo Ki=0 quando êu ê> usat.

Poco più complessa è invece l’implementazione di un regolatore cosiddetto a struttura variabile, ma in realtà con i soli parametri variabili nel tempo, in funzione dell’entità dell’errore.

Il caso della Fig. 25.5d è stato ottenuto semplicemente con i parametri variabili (nell’esempio è stato posto Lim = 100)

Kp = Lim / (1+Abs(e))

Ki = Lim / (1+ e²) con la condizione If Ki > 10 Then Ki = 10

Fig. 25.5d - Risposta di un sistema con regolatore a struttura variabile (VS-PI).

Come si vede, l’effetto è di mantenere praticamente saturato il regolatore finchè non viene raggiunto un errore piccolo che porta al massimo Ki.

In tal modo l’integrazione compensa la corrispondente diminuzione dell’azione proporzionale e l’effetto complessivo è di raggiungere più rapidamente possibile (comunque il massimo fisicamente permesso) un errore abbastanza piccolo e poi eliminare anche questo mediante l’azione integrale.